研究者对生态网络系统中的集体动力学行为进行数值模拟和理论分析,发现了一种新的同步现象,并将其命名为“同步中的同步”。而且,随着时间的演化,系统可以在多个不同的同步状态中进行随机的转换。
想象一下,有一个生物群落,其中包含植物、食草动物和食肉动物三个不同的种群。由于三者之间复杂的相互作用,种群的数量——比如食肉动物的数量,会发生混沌振荡。
再想象一下,如果有10个这样的群落,在空间中形成一个闭合的环状(如下图a所示),而且在相邻和次近邻的不同群落之间,存在动物的迁徙(下图a中节点间的连线)——那么就会发生“相位同步”,即不同群落中的某一种群数量的演化趋势相同(如下图b)。
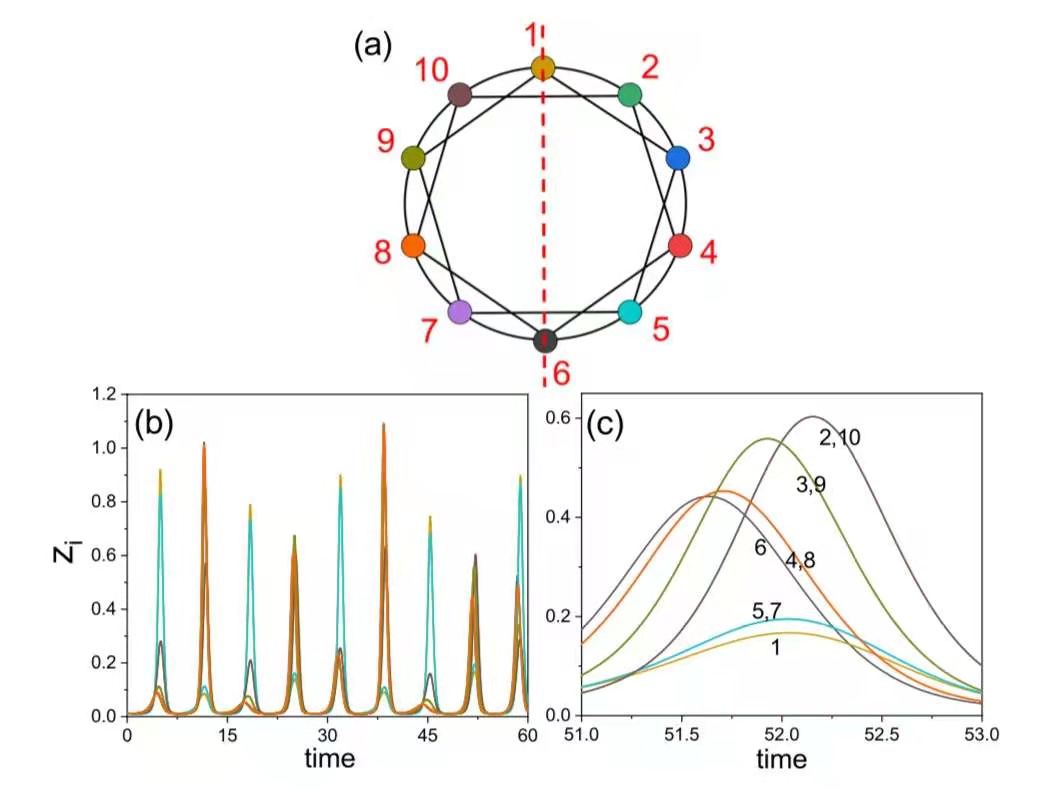
(a) 研究中采用的生态网络模型。每个节点表示一个群落,其动力学行为由经典的植物-草食动物-食肉动物混沌模型来描述。实线连线表示群落之间的耦合关系,红色虚线表示网络结构所满足的对称性;(b) 各群落中的食肉类动物种群数目随时间的演化,不同颜色曲线代表不同群落。所有群落演化在相位上达到同步。(c) 种群时间演化局部放大图。此时间段内,群落2和10在振幅上达到同步。相同现象也存在于群落3和9,4和8,以及5和7之间。
在最近发表于《国家科学评论》(National Science Review, NSR)的一篇研究论文中,研究者对前文中描述的这个系统进行了数值模拟和理论分析。结果发现,在所有10个群落达到整体相位同步之外,还存在更细致的同步模式。比如,在上图中,以1、6两个群落之间的红色虚线为对称,相互对称的4组群落(2和10、3和9、4和8、5和7)不只是振荡相位同步,而且振荡的振幅也相同(如上图c所示)。作者将这种整体相位同步中的振幅同步称为“同步中的同步”。比较有趣的一点是,在这样的对称模式下,空间上距离较远的两个群落,比如3和9,也可以实现“同步中的同步”。
而且,这样的对称和同步模式(形成“集团同步”或“同步斑图”)不止一个,以5-10、4-9、3-8、2-7连线为对称轴都可以形成对称模式,从而构成不同的同步斑图。事实上,研究者利用理论计算和分析,可以预测出所有可能出现的集团同步态,并解析得到集团同步的稳定性条件。
随着时间的演进,整个系统会在不同的同步斑图之间随机切换。为了更好地研究这种动态演化,作者向系统中引入噪音,结果发现随着噪声强度的增大,同步斑图的切换变得更加频繁,但暂态同步时间始终满足幂律分布。这些结果揭示,阵发性集团同步和同步斑图切换的动力学机制在于同步暂态,从而给出了下图所示的动力学图像:
>在相空间中存在多个平权的、具有鞍点不稳定特征的集团同步态,其稳定和不稳定流形相互交错;
>系统在演化过程中沿着某一同步态的稳定流形靠近该态,但在该态附近做短暂停留后又在不稳定流形的影响下离开该态,向其它同步态靠近,从而实现不同状态之间的随机切换;
>噪声扰动缩短了停留在各个态附近的暂态时间,提高了各态之间的切换频率。
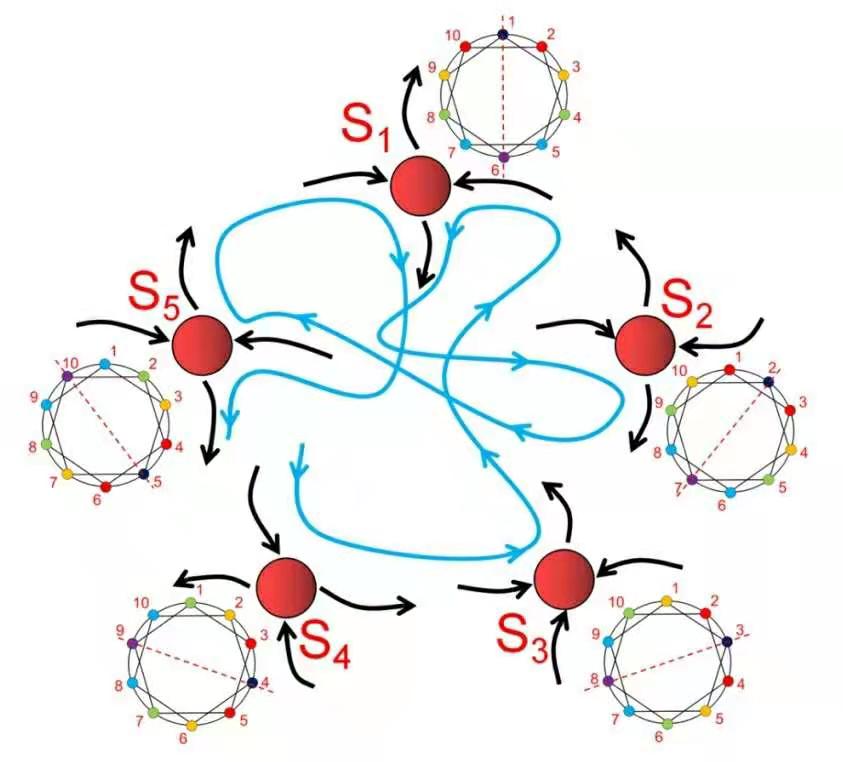
暂态同步示意图。红圈代表不同对称模式下的集团同步态。黑色实线示意各同步态的稳定和不稳定流形。各子图中的颜色相同的节点完全同步。随着时间的演化,系统在各同步态之间做随机行走(蓝色曲线)。
这项研究发现的暂态同步现象是复杂生态系统中一种独特的自组织行为,它有效调和了生态系统中稳定性和同步之间的矛盾,回答了“为什么同步振荡的复杂生态系统可以稳定存在并演化”的问题,从而为生态系统的管理和保护提供了一个全新的视角。此外,研究中关于同步集团的对称特征、遥同步现象以及同步斑图的切换演化的发现为当前复杂耦合系统集体动力学行为的研究提供了新的素材。在未来的研究中,分析其它实际复杂系统中的暂态同步行为,以及探索暂态同步与复杂系统功能之间的联系是值得关注的问题。
上述工作由det365官网网站研究团队(樊华伟博士和王新刚教授)同美国亚利桑那州立大学研究团队(孔令威博士生和来颖诚教授)以及美国加州大学戴维斯分校的Hastings教授合作完成。
文章信息:
Synchronization within synchronization: transients and intermittency in ecological networks
https://doi.org/10.1093/nsr/nwaa269
